どうもLibraです。
今回は「プログラマの数学 第2版」を読んだのでそのレビューを書いていこうと思います。出版社のページでは、私以外の多くのレビューを見たり本書の試し読みができます。下記にリンクを貼っておきますので興味のある方は合わせてご覧ください。
概要
| 著者 | 結城 浩 |
| 出版社 | SB Creative |
| 発売日 | 2018年1月17日 |
| 価格 | 2,420円(本体2,200円+10%税) |
| ページ数 | 296 |
| ISBN | 978-4-7973-9545-7 |
難易度とわかりやすさ
| 難易度 |  | 2/5 (簡単) |
| わかりやすさ |  | 4/5 (分かりやすい) |
難易度は2/5 (簡単)としました。この本は数学の話がメインですが、その内容のほとんどは高校1・2年生レベルです。数学に抵抗のない方であれば問題なく読み進められるでしょう。数学に苦手意識がある方でも、わからないところを調べれば個人で解決できるレベルの内容だと思います。
わかりやすさは4/5(分かりやすい)としました。図や数式が豊富で視覚的に理解しやすいだけでなく、プログラマ的な考え方やそのバックグラウンドまで解説されているのが良かったです。「プログラマの数学」と銘打っていますが、長いコードで埋め尽くされているわけでなく、説明が必要な箇所にのみ短いコードが載せてあるだけなので、プログラミングを勉強している方にも読みやすい内容だと思います。
各章要約
第1章 ゼロの物語 ── 「ない」ものが「ある」ことの意味
この章では0という数字が果たしている役割から、私たちが日常的に使用してる10進法、コンピュータで使われている2進法などの位取り記数法、指数法則について解説されています。
古来から人間は「認識しづらい大きな数字は小さなまとまりにして表現する」ということをしてきました。ローマ数字では5をIIIIIではなくVと表し、指数法則を用いれば1,000,000,000,000という天文学的数字も1012と簡単に表現できます。数字がどのように発展してきたかの歴史を辿ることで、「0」がどのような役割を果たしているのかが見えくるのです。
「0」が果たしている役割を踏まえたところで、プログラマにとって大事な考え方が紹介されています。それは「小さなまとまりにする」ことで、本書はこの考え方をテーマにしています。次章以降もこの考え方は姿を変えて頻繁に登場するので是非覚えておきましょう。
余談ですが「小さなまとまりにする」という考え方に加えて「パターンを見つける(作り出す)」と言う考え方も同じくらい重要かなーと個人的には思っています。プログラミングとは数学でいう「一般化」に近い行為だと考えているからです。物事を一般化するには「パターンを見つける(作り出す)」という考え方が必須であり、そういった意味でもプログラマにとって数学は特別な分野だと言えるかもしれませんね。
第2章 論理 ── trueとfalseの2分割
この章では論理と命題の話題を中心に論理式、真理値表、ベン図、カルノー図について解説されています。
大学で情報工学を専攻した方なら馴染み深い内容でしょう。この章の本質は、私たちが普段使っている自然言語やルールなど、曖昧さを多く含む現実世界の事象を論理の世界に落とし込み、単純化するということです。単純化するためのツールとして、上述した真理値表やカルノー図などがあり、それらの使い方や考え方が紹介されています。
プログラマにとって排他的(「だぶり」がない)で網羅的(「もれ」がない)であることは、とても重要なことなのです。
第3章 剰余 ── 周期性とグループ分け
剰余とは割り算の「余り」のことです。この章では余剰を用いてグループ分けができること、パターンを作り出せることが解説されています。
どういうことかというと、例えば10日後が何曜日であるかを計算する際、7日ごとに同じ曜日がやってくることを考慮して、10 ÷ 7 = 1 余り 3 と計算できるので、今日が土曜なら10日後は火曜、今日が日曜なら10日後は水曜ということがわかります。
このように、剰余には周期性をグループ化してパターンを作り出す能力があります。ここでは雑に説明しましたが、本書ではより丁寧に説明されていますので、気になった方は是非読んでみてください。
補足ですが、この章の関連事項としてパリティビットの紹介がされているように、剰余の考え方は情報理論や暗号理論の分野でも大きな力を発揮します。
第4章 数学的帰納法 ── 無数のドミノを倒すには
この章では数学的帰納法と、その考え方をどうプログラムに落とし込めば良いかについて解説されています。
本書は数字を用いた解説がメインで、プログラムを用いた解説は少ないのですが、この章に限ってはC言語を用いて数学的帰納法の解説がされています。プログラム自体は10行前後の短い物ばかりなので、C言語を知らなくても理解するのはそう難しくないでしょう。
余談ですが私が初めて数学的帰納法を習った時、内容を全然理解できなくて苦手意識を持っていたことをよく覚えています。高校や大学で使っているうちに何となく理解した気になっていて、なあなあの関係になっていたので、この章は普通にいい復習になりましたね。
第5章 順列・組み合わせ ── 数えないための法則
この章では順列、組み合わせ、集合などを用いたあらゆる数え上げの法則について解説されています。内容については高校数学とほぼ変わらないので、特筆することはありません。
第6章 再帰 ── 自分で自分を定義する
再帰処理は初見ではなかなか難しく躓く人が多い印象です(実際私もそうでした)。大学での授業やプログラミング本など、プログラムにフォーカスして再帰を学ぶ機会は多くありますが、本書のように数学にフォーカスして再帰処理を解説している本は珍しいので、再帰処理で躓いている方はこの章の内容に目を通してみと理解の助けになるかもしれません。
再帰とは自分自身を使って自分を定義するということです。ここではハノイの塔、フィボナッチ数列、パスカルの三角形を例として再帰処理と漸化式について解説されています。
第7章 指数的な爆発 ── 困難な問題との戦い
この章では指数的な爆発 ── 言い換えると「急激に数が増加する」現象について解説しています。この現象は正しく認知していないと解決不可能な問題にぶつかってしまう、もしくは問題を解決不可能なものに変えてしまう危険性を孕んでいますが、一方で解決困難な問題を解決するための強力な武器にもなります。
高度な内容で滅多に使う知識ではないと思われるかもしれませんが、システム開発の現場では割と頻繁に見かけるので、知っておくと気づけることが多くなると思います。
第8章 計算不可能な問題 ── 数えられない数、プログラムできないプログラム
少し高度な内容になりますが、ここでは計算不可能な問題 ── すなわちコンピュータが本質的に解くことができない問題について解説しています。その前段階として「背理法」という証明法と「カウンタブル」の概念について学び、次に計算不可能な問題の具体例として有名な「停止判定問題」が紹介されています。
計算不可能な問題というのは非常に難しい概念なので、「コンピュータでも原理的に解けない問題がある」ということが理解できればとりあえず十分でしょう。
第9章 プログラマの数学とは ── まとめにかえて
これまでのまとめです。加えてプログラマと数学の関係性について、筆者の考えが方が簡単に記述されています。
付録1 機械学習への第一歩
ここでは機械学習に関連した技術や、機械学習の流れについて紹介されています。浅く広く、さまざまな内容が紹介されていますので、機械学習のさわりの部分について知るには丁度良いでしょう。
付録2 読書案内
数学やアルゴリズムについての書籍が中心に紹介されています。数学が好きな方は是非どうぞ。
この本を読んでやってみたこと
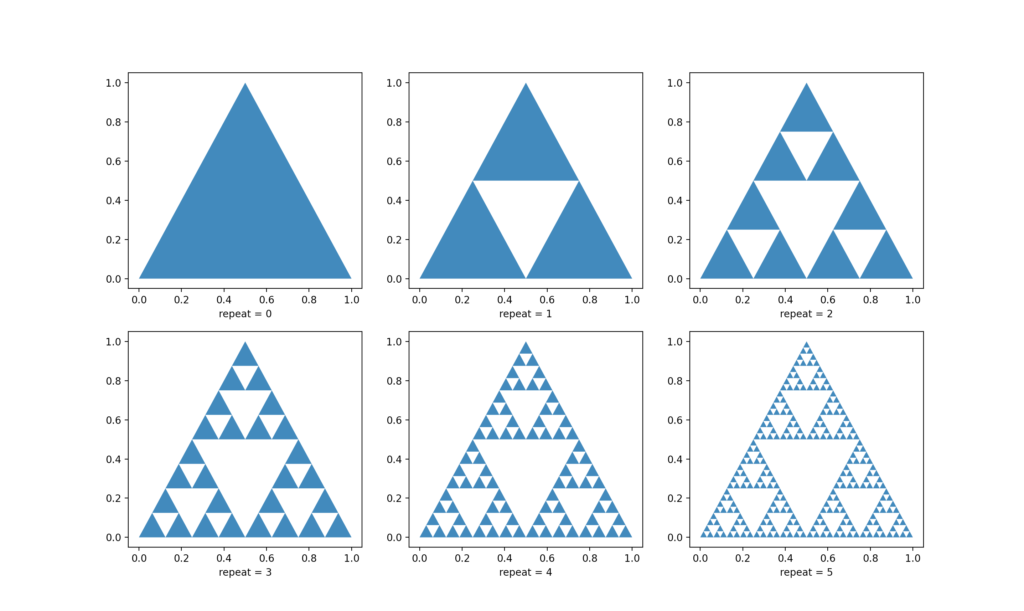
今回は本書でも紹介されているシェルピンスキーのギャスケットを描くプログラムを書いてみました。フラクタル図形のひとつとして紹介されていましたが、これを描くプログラムは本書で紹介されていなかったため、自分で作ってみた次第です。
OS: macOS Monterey 12.2
Python: 3.8.2
matplotlib: 3.4.3
import matplotlib.pyplot as plt
# matplotlibの設定
plt.figure()
plt.subplot(1,1,1)
# 三角形の初期値。青色で表示される
plt.fill((0, 1, 0.5), (0, 0, 1))
# x座標、y座標の中点を求める
def midpoint(x, y):
midx = ((x[0] + x[1]) / 2, (x[1] + x[2]) / 2, (x[2] + x[0]) / 2)
midy = ((y[0] + y[1]) / 2, (y[1] + y[2]) / 2, (y[2] + y[0]) / 2)
return midx, midy
# 指定した3点を持つ三角形を白く塗りつぶす
def fillWhite(x, y):
plt.fill(x, y, facecolor = 'white')
# 再起処理を用いてrepeat分だけ初期の三角形を白く塗りつぶしていく
def sierpinski(x, y, repeat):
if (repeat > 0):
fillWhite(midpoint(x, y)[0], midpoint(x, y)[1])
sierpinski((x[0], (x[0] + x[1]) / 2, (x[0] + x[2]) / 2), (y[0], (y[0] + y[1]) / 2, (y[0] + y[2]) / 2), repeat - 1)
sierpinski((x[1], (x[1] + x[0]) / 2, (x[1] + x[2]) / 2), (y[1], (y[1] + y[0]) / 2, (y[1] + y[2]) / 2), repeat - 1)
sierpinski((x[2], (x[2] + x[1]) / 2, (x[2] + x[0]) / 2), (y[2], (y[2] + y[1]) / 2, (y[2] + y[0]) / 2), repeat - 1)
# sierpinski((0, 1, 0.5), (0, 0, 1), 2)
plt.show()
個人的な感想
本書が第2版ということで、長く多くの人に読まれているだけのことはあると感じさせる1冊でした。学生や初級、中級のプログラマの方々には確実にプラスになる内容だと思います(情報系の大学にいる、もしくはIT系の仕事をされている方であれば、本書をすでに読んだ事があるという人も多いでしょう)。
世の中にはプログラミングに数学は必要ないと吹聴する人もいますが、私個人の見解を言えば、それは半分事実で半分嘘です。確かに数学に精通していなくともプログラムを書くことはできますが、数学に強いプログラマと、数学に弱いプログラマがいれば、多くの人は前者のような人と仕事をしたいでしょうし、実際前者のような人の方が良いプログラムを書ける場合が多いです。
近年、流行っているAIや機械学習などの分野に関しては、(付録1を見る通り)数学の知識が必須となってくるので、これからも数学に強いプログラマほど活躍できる機会は多くなりそうだと思います。
まとめ
この記事で紹介したのは各章のさわりの部分だけで、実際はここよりはるかに豊富な解説が本書でされています。気になった方は是非本書を手に取ってみてください。
今回はここまでとなります。ここまで読んでくださった皆様、ありがとうございました。


